Introduction to Recurrence

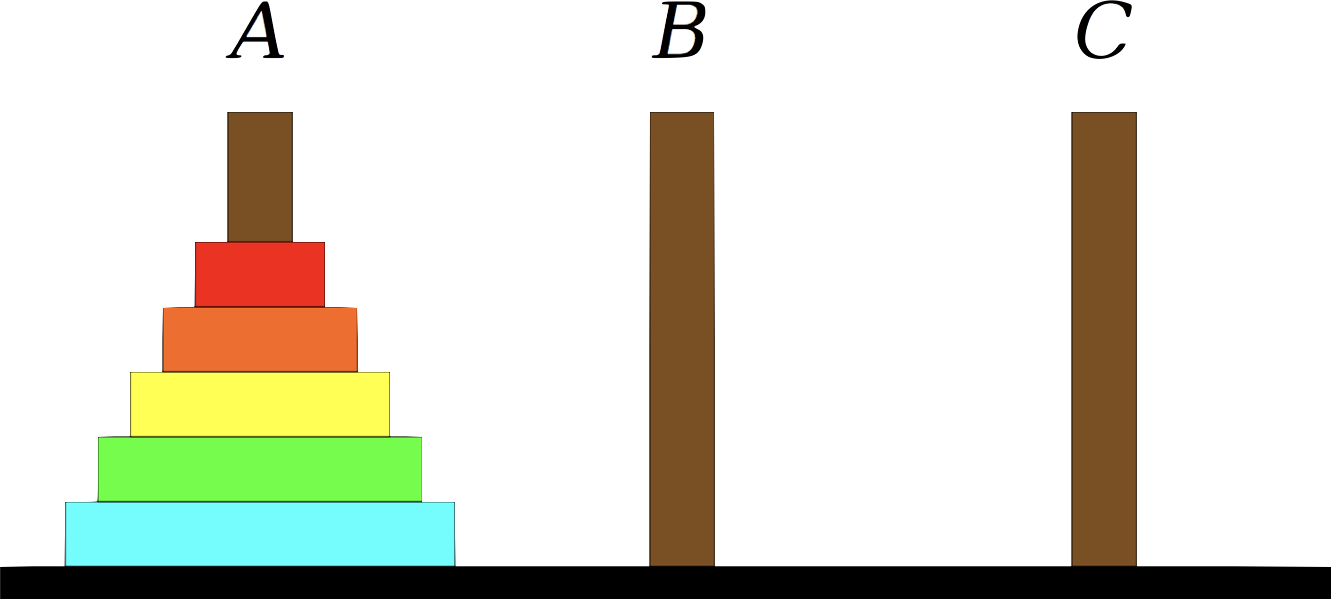
Towers of Hanoi

The problem of Tower of Hanoi is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical shape. The objective of the puzzle is to move the entire stack to the last rod, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- No disk may be placed on top of a disk that is smaller than it.
Can we solve this problem? If so how?
-
There is a simple proof that this problem has a solution.
-
What is funny is that the recursive proof is also a solution to show how.
In case you’re not convinced, here is a demo showing the result for a given size.
The main question, is that can we solve this problem using a classical approach.
At the end of this lecture you will be able to propose a rigourous and complete solution to this problem!!!
What is Recursion
Recurrence is A common method of simplification is to divide a problem into subproblems of the same type. As a computer programming technique, this is called divide and conquer and is key to the design of many important algorithms.
We could ask the question how can a solve a problem by calling the same instance of that problem. The technique rely on simplification where each call needs a simplified version of the same problem. This reduction will continue until we hit a case where we have an answer. That case is generally called base case.
Why Recursion
Recurrence offers:
- An elegant and simple solution for complex problems.
- A powerful tool for any serious programmer.
Also in life, recurrence is so redundant that have several examples like the jigsaw puzzle:

How did solve this problem?
- You use a recursive procedure:
- Find a single correct piece.
- Continue with a simplified version of the puzzle.
In order to grasp these concepts, we will follow up with some basic examples.
Counting People
We will consider the simple problem of counting the number of people in a queue.

The problem is that is each person could only talk to its neighbor. More precisely:
- each person could only talk to the person in front him and behind him.
- Solution: Using recurrence
- Each person recover the answer from the person behind him.
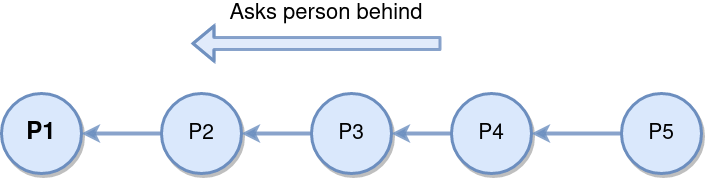
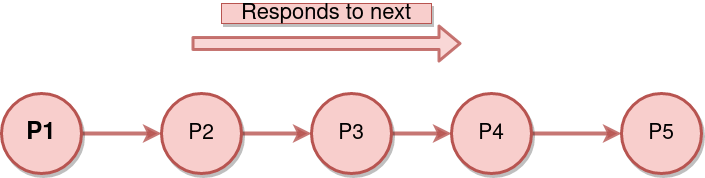
int countPersons( Person P)
{
if(noOneBehind(p))
return 1;
else
{
auto behind = countPersons(P.getBehind());
return behind + 1;
}
}
The Three Must
In order to conceive a recursive function we must have the following points:
Base case: the simple case where we have an answer.
For example, in the previous example, the person at the start knows that there is no person behind him. So the answer will be 1.
recurrence relation: comes in the heart of the problem, this is how we will reduce the size of the problem and call a simplified version.
In the previous example, the recurrence reside on the number of person will my answer plus the people behind me which I can call for neighbor to get me this answer.
convergence: you must also assure that each reduction will lead to basic case at the end.
Once all the three point are covered you take the leap of faith and be sure that your code will produce the right result.

Basic Examples
In this section, we will introduce some basic examples to grasp those concepts.
Factorial
We will consider the example of computing the factorial of an integer \(n\).
\[n! = n \times (n-1) \times (n-2) \ldots 3 \times 2 \times 1\]We could easily produce an iterative function. But we will try to produce a recursive solution.
We will deliberately produce two wrong versions. Your goal is to identify the error:
int fact(int n)
{
//base case
if ( n == 1)
return 1;
else
return n * n-1 * fact(n-2);
}
Download the code factorial.zip and add this implementation to you code to check the error.
A second version is also wrong:
int main( int n)
{
// Base case
if ( n== 0 || n == 1 )
return 1;
// Recurrence
else
return fact(n+1) / n;
}
What is the problem of those implementation?
Finally here is the correct one:
int main( int n)
{
// Base case
if ( n== 0 || n == 1 )
return 1;
// Recurrence
else
return n * fact(n-1);
}
Another intriguing question is to how to evaluate the complexity of this version.
Power of X
Another interesting example, is to implement the function power of a real \(x\) using recurrence.
float power(float x, int n)
{
//recursive function to compute the power of x and n
}
The starting project is in power.zip with simple tests.
Let’s think about the following questions:
- What is the
base case - What is the
recurrence relation - What is the
complexityof your idea.
First try
We will base it on the following relation.
\[x^n = \left\{ \begin{array}{ll} 1 & \text{if} & n=1\\[2pt] x \times x^{n-1} & \text{else} \end{array}\right.\]float power(float x, int n)
{
//base case
if ( n == 0)
return 1;
//recurrence relation
return x * power(x, n-1);
}
If we analyse the complexity of this function, we will find:
\[C(n) = \underbrace{\mathcal{O}(1) + \mathcal{O}(1) + \ldots + \mathcal{O}(1)}_{n \text{ fois}} = \mathcal{O}(n)\]Second try
A better approach is to use the following implementation:
\[x^n = \left\{ \begin{array}{ll} 1 & \text{if} & n=1\\[2pt] x^{\frac{n}{2}}\;.\; x^{\frac{n}{2}} & \text{if} & \text{n is even}\\ x\;.\;x^{\frac{n}{2}}\;.\; x^{\frac{n}{2}} & \text{if} & \text{n is odd}\\ \end{array}\right.\]Which gives the following function:
float power( float x, int n)
{
//base case
if ( n == 0 )
return 1;
// recursive call
auto val = power(x, n/2);
return ( n % 2 == 0) ? val * val : x * val * val;
}
Later we will proove that this version has \(\mathcal{O}(\log n)\)!!!
Greatest Common Divisor
Another classical problem is to compute the greatest Common divisor of two integers using Euclid formula
Here is the code pgcd.zip with some unit tests.
The solution is given by:
int pgcd(int a, int b)
{
//base case
if ( b == 0)
return a;
//recursive call
return pgcd(b, a % b);
}
Memoization
In the previous sections, we illustrated the power and elegance of the recurrence paradigm. But we must pay a careful attention to some cases where we will repeat the computation of the same cases.
Let’s illustrate the mechanism using the classical problem of Fibonacci series:
\[\text{Fib}(n) = \left\{ \begin{array}{lll} 0 & \text{if} & n = 0 \\[4pt] 1 & \text{if} & n = 1 \\[4pt] \text{Fib}(n-1) + \text{Fib}(n - 2) & & n \geq 2\\ \end{array} \right.\]The definition suggest a recursive approach which gives the following implemenatation:
int fib( int n )
{
//base case
if ( n == 0 || n == 1)
return n;
//recursive case
return fib(n - 1) + fib( n - 2);
}
Try this implementation if the project Fibonacci.zip .
You will face a problem since some cases will not finish in time. This is because this implementation has exponential complexity.
This due to some repeated computation. Let’s illustrate this for the \(\text{Fib}(4)\).
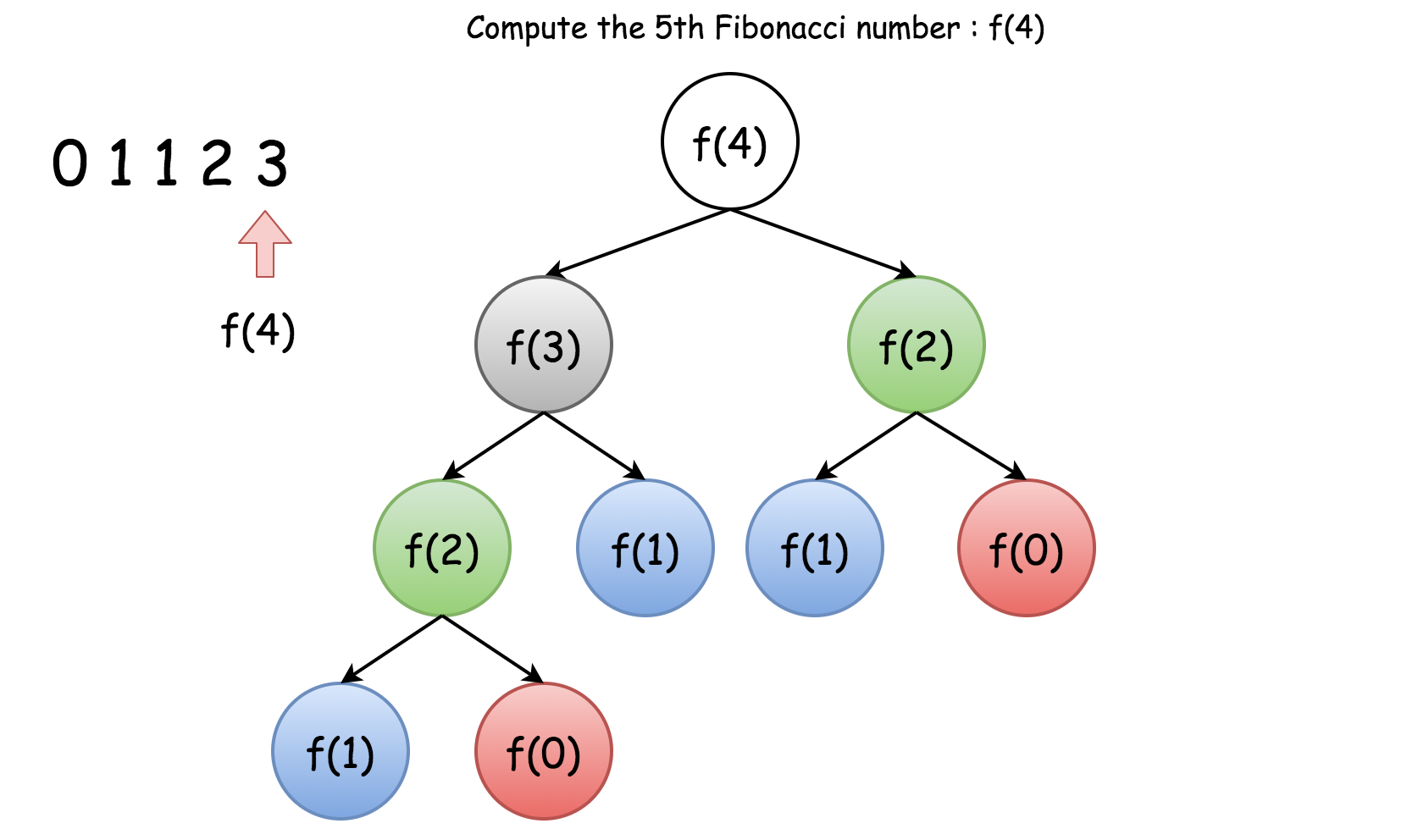
We clearly see all the repeated computation. Hence we must use a technique called Memoization in order to avoid these repetitions.
In computing, memoization or memoisation is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. Memoization has also been used in other contexts (and for purposes other than speed gains), such as in simple mutually recursive descent parsing. Although related to caching, memoization refers to a specific case of this optimization, distinguishing it from forms of caching such as buffering or page replacement. In the context of some logic programming languages, memoization is also known as tabling.
Here is a code that apply this technique reducing the time complexity to \(\mathcal{O}(n)\).
int fib_cache(int n, unoredred_set<int> & cache)
{
// Verifiy if we already computed F(n)
if ( cache.find(n) != cache.end())
return cache[n];
// recurrence
auto val = fib_cache(n - 1) + fib_cache( n - 2);
// store the computed value
cache[n] = val;
return val;
}
- This code, uses a data structure called
unordered_set. This advantage is to store keys and check for their existence is a fast way.
Complexity Analysis
The last part of this lecture covers the master theoremto compute the complexity of a recursive approach.
In the analysis of algorithms, the master theorem for divide-and-conquer recurrences provides an asymptotic analysis (using Big O notation) for recurrence relations of types that occur in the analysis of many divide and conquer algorithms. The approach was first presented by Jon Bentley, Dorothea Blostein (née Haken), and James B. Saxe in 1980, where it was described as a “unifying method” for solving such recurrences
We denote \(T(n)\) the number of operations in order to solve the recursive problem of size \(n\). If we can write \(T(n)\) as
\[T(n) = a\;T\big(\dfrac{n}{b} \big) + \mathcal{O}(n^d)\]We will have three cases:
- if \(d < \log_b a\) then
- if \(d = \log_b a\) then
- finally if \(d > \log_b a\) then
As an exercise, let’s apply the master theorem to compute the complexity of the second version of power.
float power( float x, int n)
{
//base case
if ( n == 0 )
return 1;
// recursive call
auto val = power(x, n/2);
return ( n % 2 == 0) ? val * val : x * val * val;
}
In this function, in every call we need a smaller problem of size \(\dfrac{n}{2}\).
\[T(n) = T\big(\frac{n}{2}\big) + \mathcal{O}(1)\]Hence we will have the following values:
- \[a = 1\]
- \[b = 2\]
- \[d = 0\]
To determine which case, we compute \(d\) et \(\log_b (a)\). We have
\[d = 0\]and
\[\log_b(a) = \log_2(1) = 0\]Hence, we are in the second case and the complexity is given by:
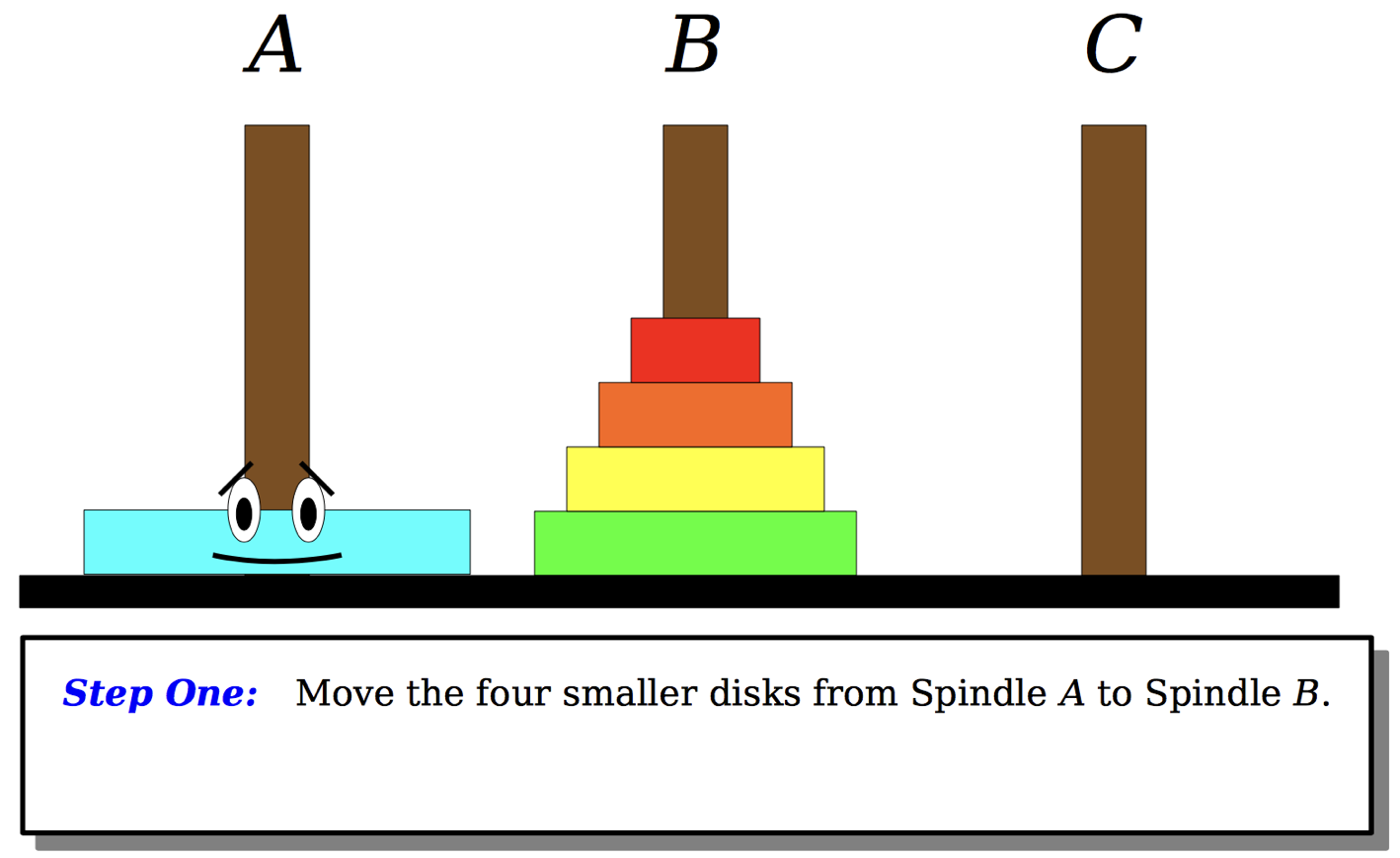
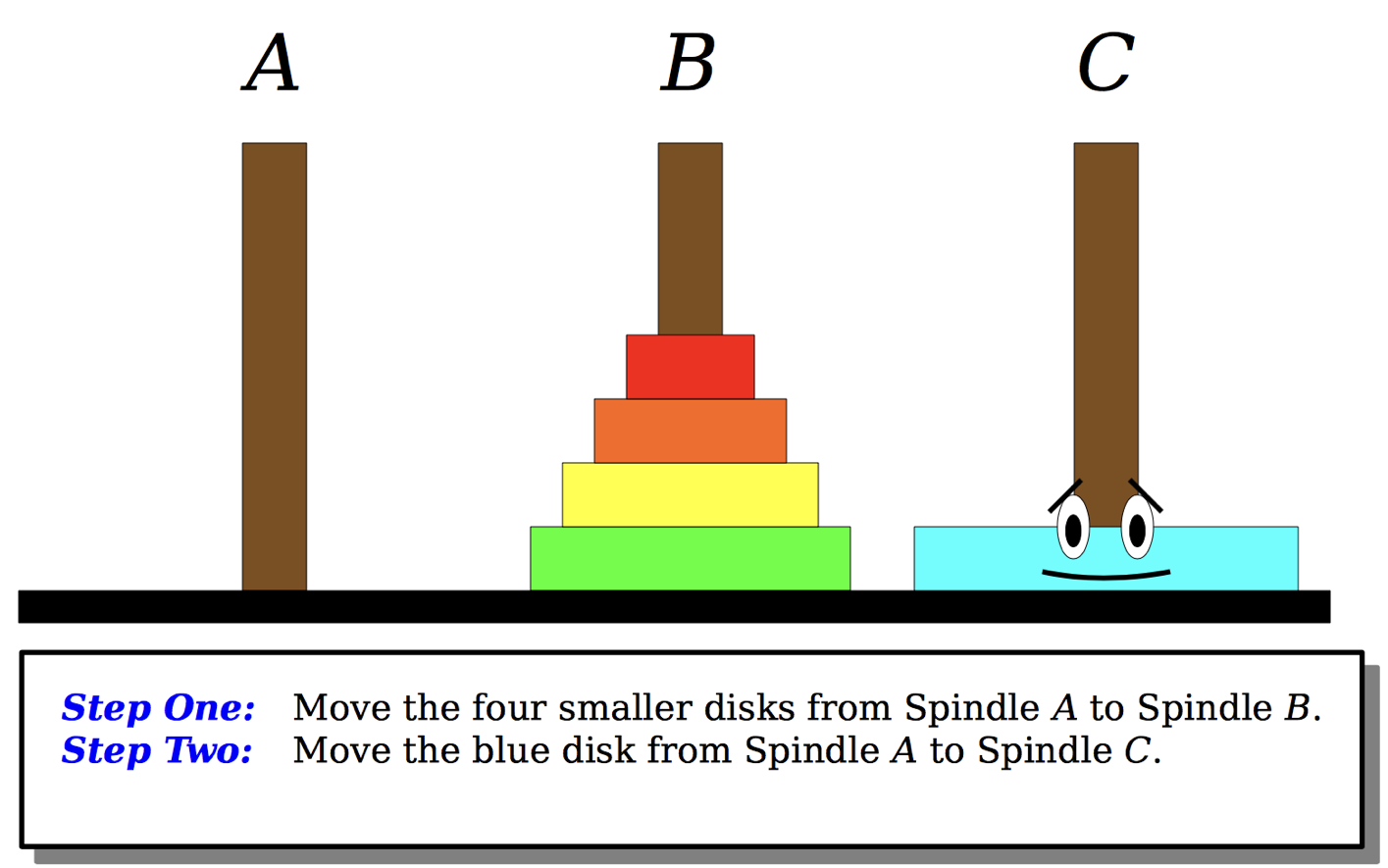
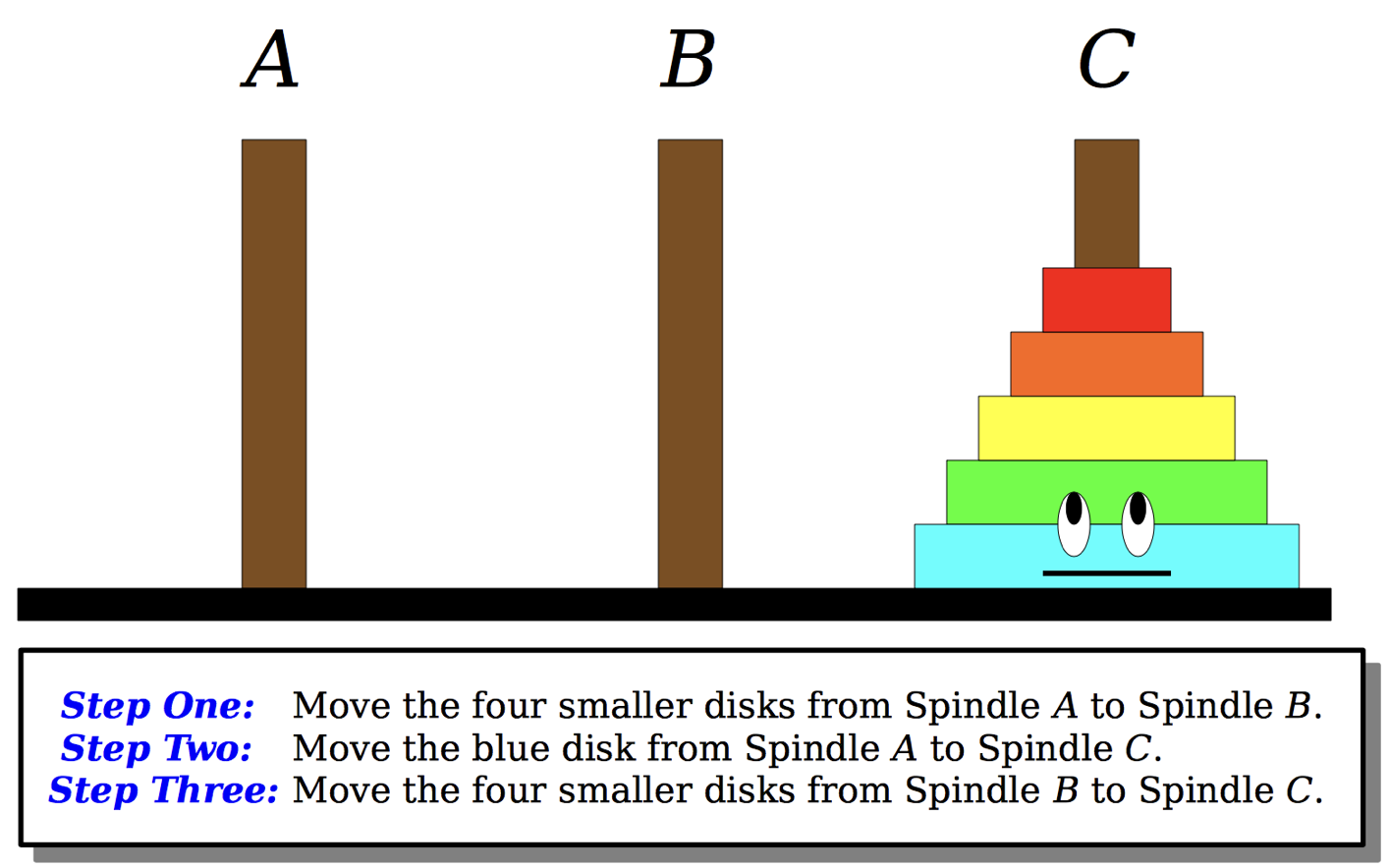
\[T(n) = \mathcal{O}(n^d\log n) = \mathcal{O}(n^0 \log n) = \mathcal{O}(\log n)\]Tower Hanoi code
Now, you have all the tools to solve the hanoi tower problem. Down lad the code Hanoi Towers.zip . and implement the function according to the following scheme: